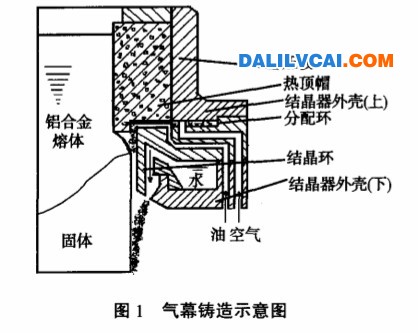
本计划前四期已发展出一套可供元富公司预测轮圈产品疲劳测试破坏、危险、或安全的计算机辅助分析程序，且已将该预测模式正式纳入元富公司的开发程序中。然而随着开发案件㈰益增加，这套计算机辅助分析程序仍然依据计划初期所统计之28笔历史测试资料进行破坏预测，对于不断增加的实测资料，无法加以适当更新以得到更准确的预测结果。此外现有的破坏预测程序对于预测结果位于危险区的案件，仅能告诉工程师此设计“危险”，无法提供更明确的量化资讯，因此我们进一步提出「机率预测模式」来取代原先疲劳破坏预测程序，以改进前述这些问题。
本文第一节将讨论旧有预测模式之优、缺点，以及实际使用上的问题；第二、三节则简介机率预测模式的设计原理；第四节介绍机率预测模式的操作接口及使用方法；最后再针对未来发展方向作一讨论。
1. 旧有轮圈疲劳破坏预测程序之优、缺点
旧有的轮圈疲劳破坏预测程序是以疲劳破坏理论搭配元富公司之历史测试数据，作为判断轮圈是否破坏之依据。如图1所示，每一轮圈经过有限元素软件作疲劳测试之模拟分析后，可以得到该轮圈在疲劳测试过程中之平均应力(mean stress)与应力振幅(stress amplitude)，便可用一个资料点代表此轮圈绘于图上，其中“×”表示实际测试破坏的轮圈，“○”表示实际测试通过的轮圈。依据元富公司所采用的铝料为A356-T6之抗拉强度与疲劳限，在此图上绘出Goodman线（如图1中的蓝色线）与Gerber线（如图1中的红色线）[Bannantine et. al, 1991]，同时在经过与元富公司之历史测试资料作对照后，订定Goodman线与Gerber线之安全系数为2.6，如此将整个预测结果划分为“Safe”、“Dangerous”、及“Failure”等三个区域，新开发的轮圈藉由有限元素分析计算所得到的平均应力及应力振幅数值，即可明确的在图中得到一个预测结果，让工程师一目了然地作为开发与否的参考依据。
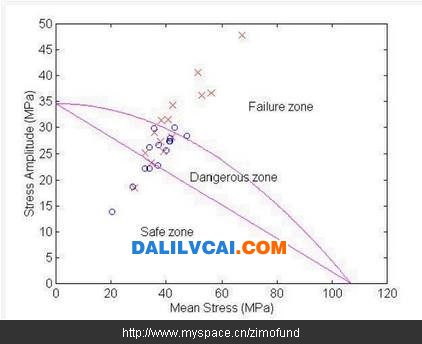图1. 旧有轮圈疲劳破坏预测程序之实际测试结果资料
然而这个轮圈疲劳破坏预测程序仍然有以下几点问题：
(1) 图1所示的破坏预测准则是一非常明确(crisp)的预测模式，安全区、危险区与破坏区的区别是分别以明确的安全线与破坏线来划分，对于在边界附近的资料点预测可能不尽合理。
(2) 在危险区的资料点仅能宣称其为“危险”，而无法提供比较明确的量化预测数据，以至于有部分轮圈的预测结果虽然位于危险区，甚至接近破坏区，工程师仍依其经验进行开发，而且实际测试合格的不合理现象产生。
(3) 对于一个制程稳定的公司而言，历史测试资料往往是最重要且最具有比对价值的，却往往也是最容易被忽略的。本预测模式却无法随着实际测试资料数不断增加而自我学习、调整，进一步提升预测正确率。
针对以上3项缺点，我们我们进一步提出机率预测模式，以元富公司不断增加的历史测试资料为比对标准，对每一个轮圈提供量化的“破坏机率”，而非破坏、危险、或安全，并以期望值的概念作为使用者对于该案件是否开发的判定依据。
2. 破坏机率预测模式
图2为元富公司至目前为止累积之50笔实际测试资料，与图1相同，横坐标为平均应力值，纵坐标为应力振幅值，“×”表示测试破坏的轮圈，“○”表示测试通过的轮圈。由此图中可以明显看到，越往图的右上方（平均应力、应力振幅越大），轮圈实际测试失败的机率也越高。
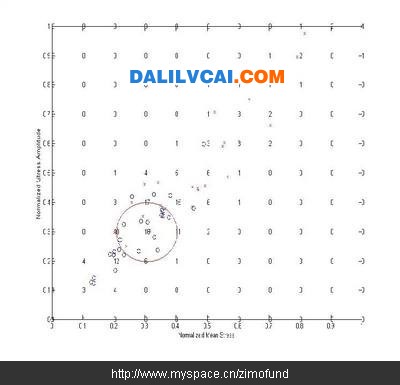
图2. 所有实际测试的结果
新开发轮圈利用有限元素分析得到其平均应力与应力振幅，便可用一个资料点代表此轮圈绘于图上，而利用历史测试资料来预测此新开发轮圈之破坏机率，最直接的想法便是，对于图2中一个新的资料点为中心画一个半径r的圆，此新资料点的破坏机率可定义为式(1)
其中Nfail为此圆内实际测试破坏之历史资料点数，Ntotal为此圆内所有资料点数。
但是如此的定义在实务上有一个严重的问题，是如何决定此圆之半径r。半径r太大时，此圆将无法精确代表此新资料点，若半径r太小时，在此圆内历史资料数可能过少，计算出的破坏机率可能没有意义。因此我们不直接以历史测试资料预测新资料点之破坏机率，而是先将历史测试资料绘成「破坏机率等高线图」，新开发轮圈之资料点绘于此破坏机率等高线图上，便可直接读出新资料点之破坏机率。
3. 绘制破坏机率等高线图
绘制破坏机率等高线图前，首先将针对所有资料点之平均应力（X轴）及应力振幅（Y轴）以式(2)予以正规化：
图3. 将平均应力及应力振幅正规化
接着将整个正规化后资料点的分布范围划分为一的网格，以网格节点为圆心画一半径为 之圆，统计此圆内测试通过及破坏之历史资料，并以式(1)计算其破坏机率 ，则此破坏机率即为该网格节点之破坏机率。如图3所示为设，后所得各网格节点之历史资料数目。图3中红色圆圈即为以(0.3, 0.3)为圆心，所绘出之圆，于此圆中共计有历史资料16笔，由此16笔资料所得之破坏机率即可被用来代表(0.3, 0.3)之破坏机率。依此方法可以计算出各网格点上之破坏机率如图4所示。注意图3中大部分的资料点分布在对角线，某些网格节点上所绘出之圆内历史资料数过少甚至没有，依据过少的历史资料点所计算出的破坏机率可能完全没有意义，因此此处设定一有效资料点数目N effective，图4中网格节点上所包含之历史资料数目少于设定之有效资料点数目Neffective，则在该网格节点上以“×”表示。图4中为设定Neffective=0，亦即所有具有破坏机率之网格节点均被使用的状况。
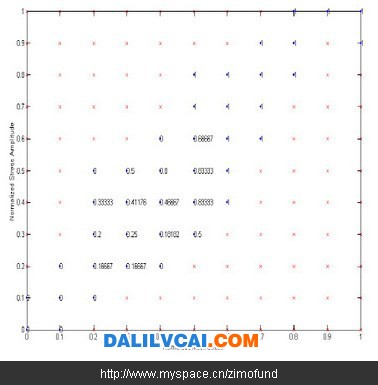
图4. 各网格点的破坏机率值
获得各网格点的破坏机率后，接下来将进一步以内、外插的方式，将破坏机率值扩展到全域，以绘出破坏机率等高线图。有效资料点数目Neffective的设定将有助于避免圆内历史资料数过少，使得计算出的破坏机率可能没有意义的状况发生。然而Neffective设的太高，将可能使得可计算破坏机率之网格节点数过少，导致后续将破坏机率值扩至全域的处理过程中，使数值演算不收敛而无法获得破坏机率等高线图。然而在历史资料数还不足时，依据少数历史资料计算出的破坏机率值有分布不平滑、甚至不合理的情况，因此在绘出破坏机率等高线图前，我们加入了两项工程上的判断规则，来先对各网格节点的破坏机率值作平滑化的处理：
(1) 位于上方节点的破坏机率恒大于或等于位于下方节点的破坏机率。
(2) 位于右方节点的破坏机率恒大于或等于位于左方节点的破坏机率。
依据该两项规则重新检视图4中各节点的机率值，其中网格点(0.4, 0.3)之破坏机率值小于其左方网格点(0.3, 0.3)之破坏机率值，显然违背上述第二项规则，因此，该节点的机率值是不合理的，必须予以删除。以此二规则删除图4中不合理的网格节点，如(0.4, 0.5)、(0.2, 0.5)等，得到修正后的实测破坏机率值如图5所示。
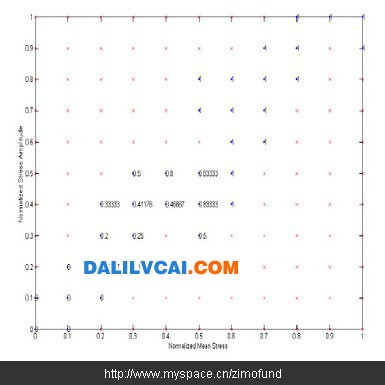
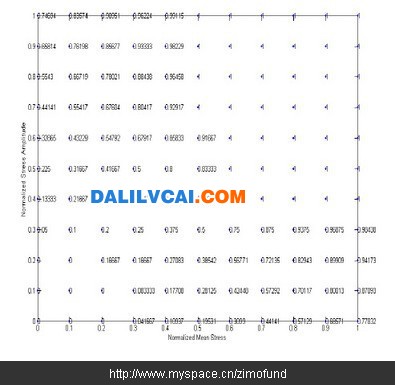
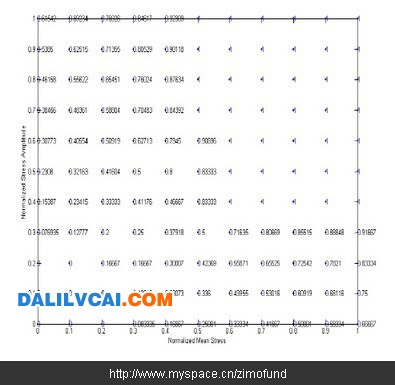图7. 最终迭代后的全域破坏机率值
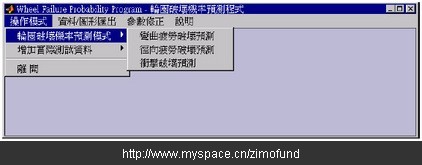图8. 破坏机率等高线图与旧有模式之比较
图9. 轮圈破坏机率预测程序之操作接口
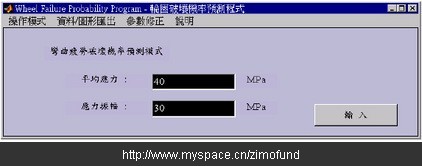
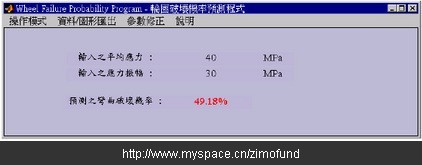
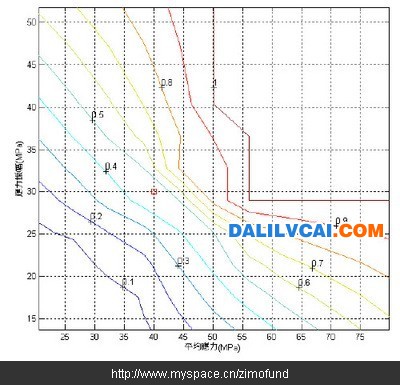图12. 预测弯曲破坏机率之等高线图形
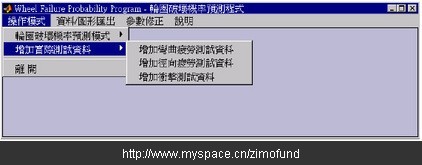
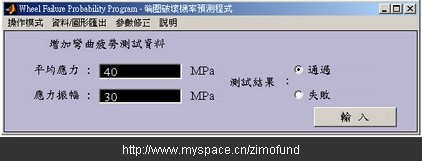
图5. 修正后的实测破坏机率值
以图5的破坏机率值为基础，接着将用内插法与外插法，将破坏机率值扩展至全域，以绘出破坏机率等高线图。注意这是一个迭代形式的过程，如图6所示为经过一次迭代，将图5中没有破坏机率值的节点逐一以线性内插或外插求出后所得的结果，新数值加入后，下一次迭代再次重新逐一检查每一节点，以线性内插的方式继续调整每一节点上的破坏机率数值，但图5中原先已有破坏机率数字之节点则不会被改变。如此不断迭代，直到所有节点上的破坏机率数字都不再变化为止（如图7）。运用图7的结果，我们即可将全域的破坏机率值绘制成等高线图，如图8所示，此图应是这组历史资料点可以产生之最平滑的破坏机率等高线图。
图6. 第一次迭代后的全域破坏机率值
图8的破坏机率等高线图，即是对图3中离散的历史资料点资料所显示“破坏可能性趋势”的一个近似、量化的表现方式。图3中大部分历史资料点都集中在对角线附近，产生新的资料点时预期也会发生在目前资料点较密集的区域，而较不会发生没有资料点或资料点较稀疏的区域。因此对于没有资料点或资料点较稀疏区域平滑化处理的主要目的，完全在于产生较平滑之破坏机率等高线图，精确度反而不是考虑的重点。
4. 对破坏机率等高线图之阐释
图8中同时标示出旧有之破坏预测模式所使用的Goodman线（破坏线）与Gerber线（安全线），可以看出原先预测“破坏”之轮圈破坏机率在0.7以上，预测“安全”之轮圈破坏机率在0.2以下，而预测“危险”的轮圈，在图8中可以读出一个量化的破坏机率数字。
对于一个新开发的轮圈，机率预测模式将根据历史测试资料预测出一个破坏机率值，与旧有明确、无弹性的预测模式有明显的不同。图8之破坏机率等高线图也随着实际测试资料的增加而不断的更新，所有的历史资料都会被有效的保存与运用。
在实际的开发经验上，对于一件新的开发案，若没有经过详细的CAE预测，则往往容易因测试的不合格而不断修改，一件开发案常常需要经过3至4次的试作才能成功进入量产。因此获得一个新开发轮圈的破坏机率值之后，是否要接受这个设计继续开发，还是应重新修改设计以降低破坏机率，这个判断和元富公司对于新开发案试作次数的期望值有关。假设每一轮圈至多于第二次测试时均可通过测试，则从机率预测模式中得到破坏机率为Pfail的轮圈，其试作次数的期望值为(1-Pfail)+2Pfail。举例来说，若公司的政策订定每一新开发件的平均试作次数需在1.3次以下，则可得到Pfail=0.3，亦即当工程师进行CAE分析以及破坏机率预测后，必须以破坏机率为0.3的等高线作为是否开模的基准，当预测之破坏机率小于0.3时，即可进行实际之开模测试。
5. 破坏机率预测模式之操作接口
图9为轮圈破坏机率预测程序之操作接口。主要操作模式可分为轮圈破坏机率预测模式及增加实际测试资料等两大部分。在预测模式部分则包含了轮圈的三大测试，即弯曲、径向及冲击测试的破坏预测，此三项测试都将以机率预测模式来作预测，其中弯曲及径向已分别有了完整的基础资料可供使用，冲击测试部分则仍待建立。
假设某个轮圈的平均应力为40Mpa，应力振幅为30Mpa。如图10分别输入平均应力及应力振幅数值后，经过与资料库的比对计算后，分别得到如图11的破坏机率值49.18%，及如图12以红色“□”表示的破坏机率等高线位置图。
图10. 输入平均应力及应力振幅数值
图11. 预测弯曲破坏机率输出结果
于前段中提到，旧有预测模式无法随着实际测试资料数不断增加而自我学习、调整，进一步提升预测正确率，因此，在机率预测模式中加入了“增加实际测试资料”的功能，其输入界面如图13所示，只要有实际测试的结果，就可以分别加以输入并更新资料库（如图14），藉由此一功能即可将实测资料不断累积，进一步提升预测的准确性。
图13. 增加实际测试资料输入接口
图14. 实测资料输入接口
