挤出铝型材稳定成形的原理分析

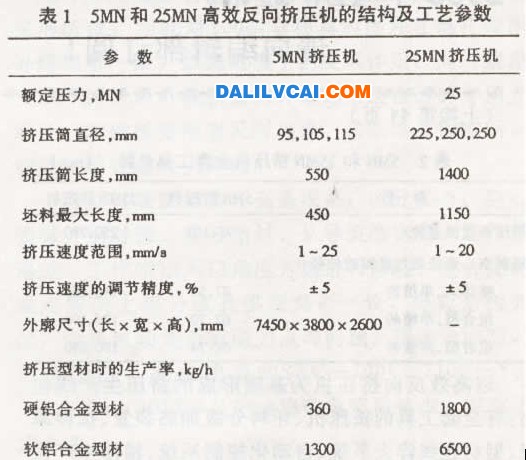
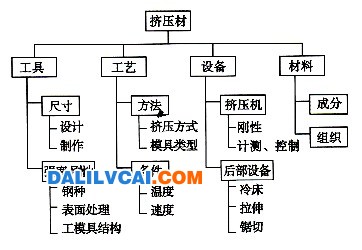
1.引言

铝合金在挤压成形过程中，由于受到挤压筒壁、模具端面、分流孔、焊合腔、工作带表面等部位的剧烈摩擦，各位置的流速是极不均匀的。当挤压形状不对称，各部分尺寸，形状相差很大的制品时，这种流动不均匀性更会显著增加。而且，在模具设计制造中，各部位流动速度的差异不可能完全的消除或调整。因此，挤压成形中，不能避免的会产生各种成形缺陷，如扭拧、弯曲、波浪、裂纹等^[1]。挤压模具在使用中，铝型材不成形、波浪、弯曲等由于金属挤出模孔速度不均匀引起的试模不合格，是造成试模不合格的主要原因之一。为了消除以上这些缺陷，最理想的结果就是金属在挤出模孔时，各个部位各个质点的金属流动速度均保持一致。而实际的情况是，金属在挤出模孔时，即使最简单的铝型材也不可能各个质点都获得相同的流动速度。因此，必然存在一个速度差异范围，当金属挤出模孔时，当各个质点的挤出速度差异在这一个范围之内时，挤出的铝型材能够稳定成形。

2.稳定成形机理分析

根据最基本的金属塑性成形原理，金属在塑性变形时，总是向着变形阻力最小的方向流动。因此，金属的应力状态是影响金属流动变形的根本因素。在挤压成形出材的过程中，常见的一些成形缺陷，如波浪、扭拧、侧弯等，形成的根本原因是挤出的金属的应力负载超过了保持其原来稳定状态的临界应力，从而使挤出金属发生弯曲、皱曲、扭转等变形。

对于挤出模孔的金属，一般情况下，只受到模孔出口截面的约束作用，在其它方向、位置上均处于自由状态（忽略了与挤压方向垂直的重力作用和挤压牵引设备的支撑力作用），如图1所示。而在离模孔出口足够远的位置，金属的塑性成形已经完成，因此，考察挤压成形出材的稳定性，只需对从模孔出口以外的一小段进行考察。

以简单的扁条铝型材为例，对挤出模孔的金属进行受力分析。对于挤压成形的铝型材而言，铝型材的壁厚相比各铝型材壁面一般较小，可看作为薄板。

若金属挤出模孔各位置的轴向速度完全一致，即v_xi v_out，且v_yi0  (1)

则挤出部分的金属各部位的流动应力相等，金属不发生变形。

    若金属挤出模孔各位置的速度不完全相等，假设中心位置的金属挤出较快，假设BC段的速度为v₁，边缘位置的金属流动速度较慢，AB、CD段的速度为v₂, 有v₁ > v₂，如图2(1)所示。在一个很短的时间Δt后，BC段沿着挤压方向向前运动了v₁ Δt，到达B'C'，而AB、CD段则沿着挤压方向向前运动了v₂Δt，到达A'B''和C''D'位置。如图2(2)所示。

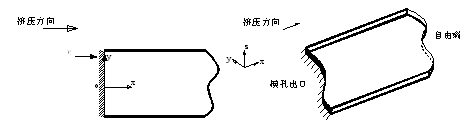
a) 水平视图                                 b)轴侧视图

图1 挤出模孔金属

Fig. 1 Extruded metal

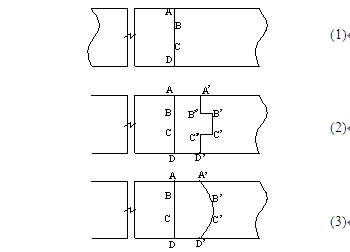
图2 出材成形原理

Fig. 2 Principle of extrudate deformation

又根据金属塑性变形的连续性条件，B'点和B''点应该是同一个点。而在图2(2)的变形过程中，B'C'段比A'B''段和C''D'段多向前运动了B'B''的距离。因此，在金属挤出模孔经过时间Δt后，“伸长”较多的BC段金属将受到其前方已挤出金属的挤压应力σ_p，从而限制了挤出较快的位置金属的挤出；而“伸长”较少的AB、CD段则受到已挤出金属拉伸的应力σ_d，促进挤出较慢位置的金属的挤出，从而使快慢两部分的金属维持相同的速度挤出，保证金属整体上的挤出变形连续，如图2(3)所示。

在出口位置挤出模孔较快的壁面上，金属受到压应力的作用；而挤出模孔较慢的壁面上，金属则受到拉应力的作用。又由于金属的变形和负载都是连续的，在“快”和“慢”之间，必然有一个临界于“快”、“慢”之间的位置，即图2(3)中的BB'连线和CC'连线的位置上，金属既不受拉亦不受压。在F. Halvorsen和T. Aukrust的研究^[2]当中，分析了薄板铝型材挤出后各位置的金属流动速度分布。得到了其分布规律符合A+Be^-C的形式。如图3所示（图中，x轴表示铝型材截面上某点到中心轴线的距离，y轴是对应该点的速度），再定义：

Δv_c v­_max- v_mid         (2)

Δv_t v­_mid- v_min      (3)

Δv_λ Δv_c(1- e^-1)     (4)

  (5)

其中，v_max为出口截面的最大速度，v_mid为壁面上应力载荷为0的临界面上金属的挤出速度，λ为距离最大速度位置的特征值，定义特征应变速率^[2]，

        (6)

x为相应点到铝型材中心位置的距离。图3的实线为数值模拟获得的曲线，而虚线为对应的式(5)指数函数的分布曲线，两者有较好的吻合。

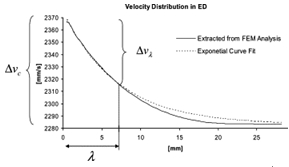
图3 薄板铝型材挤出方向的速度分布^[2]

Fig. 3 Plot of the velocity distribution in the extrusion direction along the symmetry plane

3.塑性屈曲问题

板壳的理论当中，经典的稳定性定义^[137,138]是在外载不变的情况下，若经过一个微小的扰动，结构从一个平衡状态转到另一个相邻的平衡状态，则原来的平衡状态是不稳定的。若扰动除掉后结构仍能够回到它原来的平衡状态，则这种平衡状态是稳定平衡的。

对于高温下铝合金挤压成形出材失稳的问题属于板的塑性屈曲问题。板的塑性屈曲远比弹性屈曲复杂，它必须考虑非线性的物理关系^[4]。对于板的塑性屈曲这样的非保守问题，一般只能采用动力准则对屈曲进行判定，即在有限n维空间内建立某力学系统的动力平衡方程，以u_i(i=1,2,…,n)为系统广义的位移，为相应的广义速度。若对于广义位移和广义速度在某幅度范围内的任意初始值，求解初值问题得到的所有时刻下的和都小于某指定的值和，则系统是平衡稳定的^[3]。然而动力准则在应用上仍有许多重大问题有待于解决，因此，往往仍是通过在弹性屈曲临界应力载荷上添加折减系数等方法进行处理。在本文的分析中，以式(7)的临界应力估算式作为屈曲载荷的判定公式。

          (7)

其中，k为临界应力系数，η为塑性折减系数，β为铝型材的形状系数，E为材料的弹性模量，μ为材料的泊松比，t为铝型材壁板的壁厚，b为铝型材壁板受压区域的宽度。

根据前面的分析，铝型材壁板受压区域的宽度b与铝型材壁板的宽度L是两个不同参数。在挤压出材壁板的截面上，既存在受压的区域同时也存在受拉的区域。而受压区域的宽度b与铝型材壁板的宽度L以及出口截面的速度均匀程度的分布情况有关。在其它因素相同的情况下，b随着L的增大而增大。由于受压区域的宽度b在实际挤压过程中无法测量，故式(7)难以进行应用和对比，而b与铝型材壁板的宽度L之间近似的具有线性关系，因此近似的认为一个壁面上受压和受拉的区域各占50%，则有 b=L/2。由此可见，当铝型材的壁厚越小，对应位置的壁面越宽时，铝型材产生皱曲、波浪等缺陷的可能性越大。

式(7)中的铝型材形状系数β与铝型材截面的复杂程度有关，铝型材截面交错的壁面越多，则不同壁面之间相互的约束越大，某一壁面产生皱曲需要的临界载荷则越大。因此，对于简单的薄板壁面，β = 1。而对于一般的常见铝型材，β在1.3~1.6之间取值；对于复杂截面的铝型材，β可取到2~2.5。

又对于图2薄板铝型材出口初始位置的ABCD面，挤出速度的快慢是由挤压模具的结构因素等决定的，即ABCD面的速度大小分布是稳定的。而挤出速度场的快慢差异越大，BB'和CC'之间金属的挤出量将越来越多，BC段金属维持原来的稳定的挤出形成的压应力σ_p越来越大，同样AB、CD段的拉应力σ_d也越来越大。因此，由于速度差异引起的铝型材壁面上的应力最大值若仍小于铝型材各壁面的稳定临界载荷σ_critical，则铝型材保持稳定成形。若其应力最大值超过了临界载荷σ_critical，则在应力场超过临界载荷的铝型材壁面，可能发生失稳的现象，即产生波浪、弯曲的缺陷。而对于薄板构件的稳定性问题，结构中的压应力是影响构件稳定性的主要因素，构件中的拉应力往往不会引起系统的失稳、皱曲。因此，挤出铝型材稳定的条件应表述为：

σ_pmax ≤ σ_critical         (8)

综合式(7)、式(8)，可以发现铝型材薄板的屈曲与铝型材的壁厚t、铝型材壁面的宽度L有密切的关系。铝型材的壁厚t越大，铝型材壁面的宽度L越小时，对应壁面的稳定临界载荷越大。

4.结论

在F. Halvorsen和T. Aukrust对挤压成形屈曲产生机理的研究上进行了更深一步的研究，结合塑性屈曲理论，以临界应力估算式作为屈曲载荷的判定公式，提出了挤出铝型材稳定的条件。铝型材的壁厚t越大，铝型材壁面的宽度L越小时，对应壁面的稳定临界载荷越大。(1) 结构中的压应力是影响构件稳定性的主要因素，构件中的拉应力往往不会引起系统的失稳、皱曲。

(2) 铝型材薄板的屈曲与铝型材的壁厚t、铝型材壁面的宽度L有密切的关系。铝型材的壁厚t越大，铝型材壁面的宽度L越小时，对应壁面的稳定临界载荷越大。