铝合金型材挤压技术是一种金属近净成形技术,挤压成形得到的型材产品,仅需少量加工或不再加工,即可达到产品的使用要求,具有精确的外形、较高的尺寸精度、形位精度和较好的表面粗糙度。铝合金型材挤压成形属于金属热塑性成形,成形过程受成形速度、成形温度、变形程度等多种因素的影响。由于金属热膨胀、模具弹性变形、金属流动快慢等原因,模具成形部位的尺寸和产品最终要求获得的尺寸并不完全相同。在实际设计生产制造中,模具的成形尺寸往往是由设计人员按照常规设计经验确定。但随着铝工业和挤压技术的发展,对挤压产品尺寸精度的要求越来越高,对产品的公差范围、平面度、垂直度等几何尺寸要求限制越来越严格。因此,由于尺寸精度超差,表面质量等因素造成模具不合格的比例在不断增加,已经成为铝合金挤压模具设计制造中急需解决的问题。传统的经验设计方法通过以往的经验,“大致”的确定模具的预变形量,加工制造出模具后再通过试模、测量的手段,检查型材产品是否达到尺寸要求,未能达到要求的模具再对尺寸进行修正调整,直至模具达到设计要求。整个过程属于一个试错的设计过程。
这样的设计方式往往会导致模具生产维修成本的增加,有时甚至会由于尺寸预留的不到位,导致模具报废。本文通过数值模拟的手段,对复杂的型材模具在工作条件下的弹性变形进行定量的分析。通过数值分析手段,能够对模具的弹性变形定量的作出判断和设计,从而大大的提高设计的成功率,降低生产成本。
1. 模具设计方案
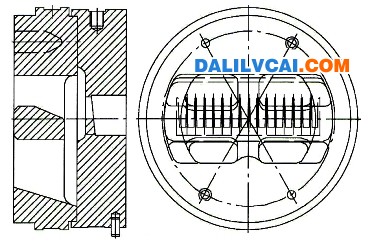
图1(a)所示是一个具有多空心结构的复杂的型材产品。产品未标注位置的壁厚要求为2.0mm。检验以上下公差 mm之内为合格产品。
图1(b)为模具设计方案主要结构示意图。模具整体外形尺寸为Φ220×140mm,其中上模总高为97mm,上模厚度为70mm;下模总高为77mm,装配外形尺寸为70mm,焊合室深度为15mm,模具工作带高度分布如图1(c)所示。
由于铝合金挤压成形是在四、五百多摄氏度的高温下进行,而成形后的型材产品一般是在常温下使用。因此,产品的尺寸在检验时需要在常温下满足尺寸要求。在确定模具尺寸时,首先要对金属挤出后的冷却收缩预留余量。又由于在工业生产中,型材壁面尺寸超负差只需要对尺寸要求超差的模具进行打磨或切割将模孔出口的尺寸加大,修理或调整较为简单;而若尺寸超正差,进行尺寸调整时则需要在模具上补焊上金属材料,再重新进行线切割、打磨等工序,修整费时较多。所以在预留尺寸余量时,尽量靠近尺寸要求的负公差尺寸进行预变形。在本次试验中,首先在产品要求尺寸各壁面上,按原产品图纸要求,先对型材整体作比例为1.01的放大,再对型材各个壁面的壁厚增加0.05mm作为试验模具的尺寸。挤压过程中铝合金坯料的预热温度为480°C,模具的预热温度为430°C。挤压速度设定为3mm/s。
2. 模型的建立
2.1几何模型
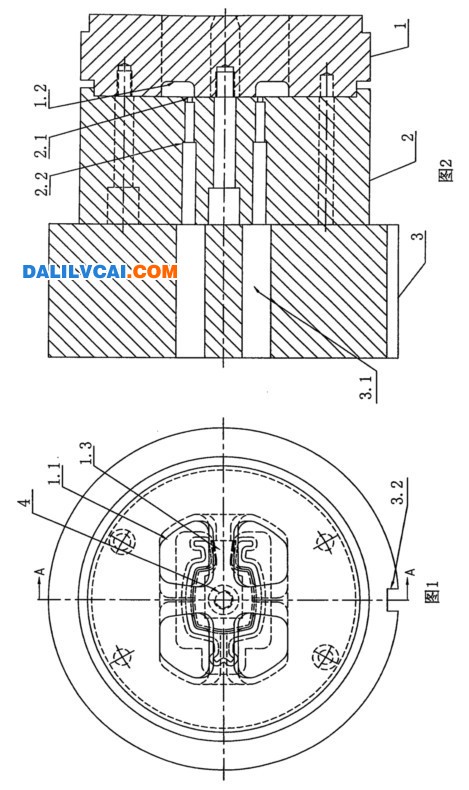
计算模型根据材料的不同分为两个部分,变形体部分和模具部分。而变形体又根据金属流动的不同区域,可分为挤压棒料区,模腔区,工作带区和型材区四个区域。其中前两个区域采用四面体四节点单元,后两个区域采用三棱柱六节点单元。而对模具部分,模具与变形体接触部分的网格节点与变形体的网格节点重合,模具部分采用四面体四节点单元。装配后的有限元网格模型如图2所示,模型的网格单元总数为1315812个,节点总数为403389。
2.2 数值模拟的基本理论
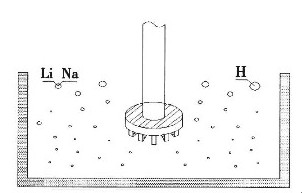
对于铝合金在挤压过程中的金属流动过程,采用任意拉格朗日欧拉法(ALE)对其进行描述。任意拉格朗日欧拉法[1-2]的思想是将计算网格定义为独立于物质构形和空间构形的参考构形,以及相应地将计算网格点定义为独立于物质点和空间点的参考点,即在ALE描述下计算网格的运动是独立且自由的,如图3所示。
在常规的Lagrange方法中,材料的运动可用下式给出:
x = Φ (X, t) (1)
式中,X是物质坐标,函数Φ (X, t)将物体从初始构形V0映射到现时构形或空间构形V。在ALE描述中,将其称为材料运动。
在Lagrange描述中,参考构形是某个时刻的真实构形;而在ALE描述中,采用的是另一类用户设计的参考域 ,如图1所示。这个域称为ALE域。在这个域中点的位置用χ表示,χ也称为参考坐标或ALE坐标。它与物质坐标的关系是:
χ = Ψ (X, t) (2)
参考域的初始值为初始构形时,即
χ = Ψ (X, 0) = x = Φ (X, 0) (3)
用参考域描述网格的运动,独立于材料运动。在ALE描述中,网格的运动可以表示为
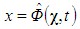 (4)
(4)
即ALE域 内点χ到空间域V中的点x的映射。
2.3 材料模型
本文的研究中,对于6063铝合金,采用双曲正弦流变应力模型[3-4],如式(5)所示,各参数的取值如表1所示。
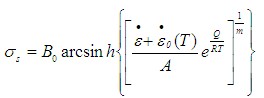 (5)
(5)
其中,R是气体常数,T是温度,B0为应力常数,A为应变因子的倒数、Q为激活能,m为应力系数。 是初始应变速率,其取值取决于温度场的给定。
对于模具材料,采用使用最普遍的是热作模具钢4Cr5MoSiV1,也称H13钢。铝合金型材挤压模具在工作时,在热应力和机械应力的作用下,主要是发生弹性变形,当模具的设计方案不合理或者由于其它原因,负载较为恶劣时,模具局部位置或者会发生塑性变形,导致模具失效。模具材料在弹性变形范围内时,其应力分量与应变分量之间满足广义虎克定律。材料的各性能参数如下:
弹性模量 E = 210 GPa;
材料密度 ρ =7.870 × 103 kg?m-3;
泊松比 ν = 0.35;
比热 C = 460 J/kg?°C;
热传导系数 k = 24.3 W/m?°C。
2.4 试验方案
本次试验模具外形装配尺寸为Φ220×140mm。根据挤压设备的使用规范以及试验条件,挤压试验选择在1300T的挤压机上进行,如图4(a)所示。挤压坯料采用棒径为Φ150mm的6063-T5铝合金铸棒。挤压试验挤压杆行进速度设定为5mm/s,坯料的预热温度为480°C,模具预热温度为430°C。图4进行试验后模具实物图。
3. 结果与讨论
3.1挤出速度结果
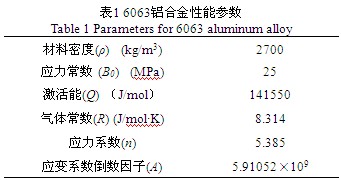
将型材按如图5(a)划分为53个不同的区域,分别截取各个区域的中心位置单元节点的金属挤出速度数据,速度场云图与取得数据曲线列于图5(b)。型材整体的挤出平均速度为97.4mm/s,计算得到的RSDV值为28.2%。出口的速度场差异偏大。而再对型材各壁面的挤出速度进行分析,发现FG,EN和AG边的挤出速度偏大,而CK,JL,BJ,DM边的挤出速度偏小。
从图5(b)可以看到,型材在模芯中间部位B到F边的挤出速度变化最大,而其它壁面的速度差异并不大。从图5(c)可以得到,型材整体左边部分的挤出速度比右边部分快,底边部分比顶部快。
图5(d)为挤压试验的获得的料头样板。挤压料头的左边壁面对应的图5(c)左边G-F-E-N的壁面,试验结果该处位置的金属挤出速度最快,使料头产生从左往右的偏转。中间位置对应的是图5(c)右上方的模芯部位,试验结果该部位的金属挤出的速度最慢。实验表明,数值模拟结果与实验结果有很好的吻合。

3.2 铝型材尺寸结果
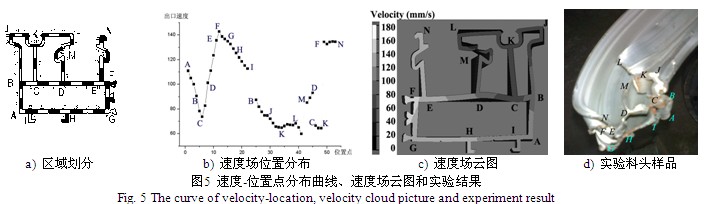
图6(a)所示为挤压实验截取的型材样板截面,图6(b)所示为数值模拟的模具的变形结果。从挤压试验的样品结果可以发现,铝型材能够稳定成形,各型材壁面的平直度均能够达到生产的要求。由于本次试验型材的壁厚在1.2mm到2mm之间,而型材截面最宽的壁面为AG边的壁面,为44mm,而且在AG边中间分别有两处装配卡脚,整个型材没有很宽的平直壁面,因此铝型材结构的出材稳定性能较好,容易获得平整的铝型材产品。所以虽然计算的速度场均匀性较差,但实际的挤压结果仍能获得平整的型材产品。
在图6(a)中,以左边平模位置的壁面为基准,将该壁面放置在正90°的位置,图6(a)中的深色实线为通过基准线偏移或者垂直获得的参考线。从图中可以看出,左上方的空心截面有明显的逆时针方向的偏转;右上方的空心截面则有微小的顺时针方向的偏转;下方的空心截面有微小的逆时针偏转,并向左侧偏移。对比图6(b)的模具模芯变形情况的模拟结果,可以发现模拟结果的变形趋势与实验结果相同。
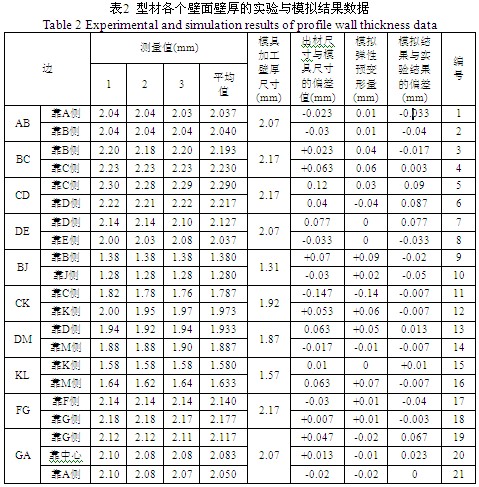
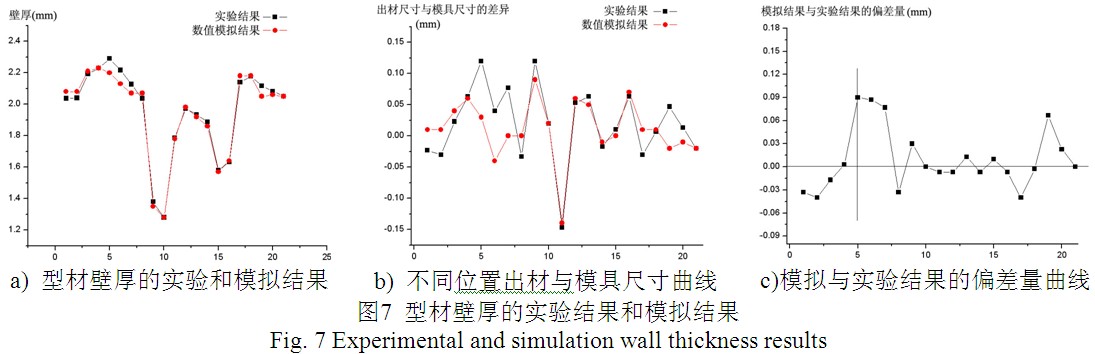
再同样按照图6(a)对型材各边的划分,对各条边的壁厚的实验结果和模拟结果进行测量,得到表2、图7结果。图7(a)为不同位置的壁厚实验结果和模拟结果的对比,其中,横轴对应为表2的编号,纵轴为型材壁厚。从图7(a)可以看到,实验结果和模拟结果吻合良好。又由于铝合金型材产品对壁厚的公差要求在 mm之间,而型材的壁厚在1.2mm到2.0mm之间,两者之间数量级相差较大,为了更准确的比较实验的测量结果与数值模拟结果。将最后的型材产品的壁厚减去对应位置模具的壁厚间隙,得到图7(b)的曲线,同样的横轴坐标为表2给定的编号,纵轴为出材尺寸和模具尺寸的差值。图7(c)所示为实验结果与模拟结果之间的偏差量,对照表2,偏差最大的位置发生在CD边上,为0.09mm。其它位置的实验结果与模拟结果的偏差都在0.05mm范围之内。可见,数值模拟结果可以较好的反映模具实际的弹性变形情况,与实验结果相吻合。
3.3 模具负载
计算获得的平均挤压力为9.10MN。模具最大应力负载为757.4MPa。而4Cr5MoSiV1热作模具钢在400°C到550°C条件下的屈服应力大约为1000MPa,因此,模具在挤压使用中处在安全的范围之内。图8(a)所示为距离入料口65mm截面模具的应力分布情况,图8(b)为与AG边平行的中心截面的应力分布情况。从结果可以看到,在型材顶角A对应的分流桥根处承受的应力最大,角J和角G对应的分流桥根处次之。三个部位属于模具可能失效的最危险位置。这与挤压基本理论和实践经验相吻合。

4. 结论
将任意拉格朗日欧拉法(ALE)和弹塑性有限元理论应用于铝合金挤压成形及模具的数值模拟研究,对一款典型的非对称多模芯的铝型材截面的模具弹性变形对铝型材壁厚的影响,以及金属的流动和模具的应力负载进行了详细的分析,模拟和实验结果吻合良好。从分析可见,通过数值模拟结合经验设计,对复杂铝型材模具的壁厚定量的预测变形的设计方法,能够有效的提高铝型材产品的设计精度和成功率。并且对特定的铝型材形状,其出口的速度波动在一个对应的范围之内时,铝型材能够稳定成形。
(1)提出了一种以数值模拟方法对模具在工作条件下的弹性变形,通过准确的数值分析,能够对模具的弹性变形定量的作出判断和设计,从而大大的提高设计的成功率,降低生产成本。
(2)对一款典型的非对称多模芯的型材截面的模具弹性变形对型材壁厚的影响进行了详细的分析,有限元模拟和实验计算结果对比,误差在0.09mm范围之内,证明了该种方法在复杂模具的弹性变形预测设计上的可行性和准确性。
(3)从本文金属流动速度场的分析可以发现,金属挤出模孔速度的均匀性不是型材成形的唯一条件。虽然挤出模孔的料头试件速度不均匀,但型材最终仍能稳定出材,可见对特定的型材形状,其出口的速度波动在一个对应的范围之内时,型材能够稳定成形。