复杂空心铝型材挤压过程金属流动数值模拟实战

引言

铝合金挤压过程是一个处在高温、高压、复杂摩擦状态等复杂条件下的金属流动成形过程。铝合金型材挤压成形工艺中理想的材料流动结果应该是在工作带出口处断面上各质点的速度均匀分布，进而获得端面平齐、壁厚均匀、产品性能能够满足需要的挤压件。

金属的流动状态对产品尺寸有很大影响，一般情况下，金属流动快的部位材料供应充足，型材壁厚是增大的，而金属流动慢的部位材料供应不足，型材壁厚是减小的^[1]。因此，在模具设计中，金属流动状态对产品尺寸的影响也是必须考虑的。在组合分流模中，由于分流孔的形状、布置以及分流桥的结构是影响材料分配的重要因素，因此，分流模中各个位置金属的流动状态所引起的产品尺寸不合格的情况尤为常见。其解决方法是：设法改善金属在模腔内的流动状态，例如改变分流孔的大小和布置、桥的结构形式都有助于改善金属在模腔内的分配，尽量使空心部分的几何中心与模具中心一致，壁厚较大的实心部分尽可能安排在桥底；另外，在合理布置分流孔的前提下，工作带的选择也可以有效调整金属流速^[1-4]。

本文利用HyperMesh对一复杂空心型材划分网格，并采用MSC.Marc对挤压成形过程进行数值模拟，在模拟过程中采用了一种既可以避免网格畸变和重划分，又能保证分析准确性的有限元模拟方法，通过模拟结果研究了金属在模腔内的流动规律，揭示了金属的流动速度对产品形状及尺寸的影响，并将模拟结果与试模结果进行比照分析。

1 采用的基本理论和方法

铝合金型材挤压成形过程是一个非常复杂的热-机耦合的弹塑性变形过程，但塑性变形远大于弹性变形，因此忽略材料的弹性变形，而将其看作刚塑性材料来处理。刚塑性材料在塑性成形过程中应满足平衡方程、几何方程、本构方程、屈服准则、体积不可压缩条件及力和速度边界条件。而用有限元法模拟非线性的铝型材挤压过程时，由于变形量大，会不断发生网格畸变，需要进行网格重划分，这样不但耗时，损失计算精度，而且过度畸变的网格在重划分时往往出现失败，使得模拟无法完成^[5-7]。

为解决拉格朗日有限元法在计算大变形挤压成形过程中发生的网格畸变和重划分问题，本文设定很小挤压时间和计算步长，将整个计算过程控制在网格由于过度畸变而需要网格重划分之前，大大提高了计算精度。

2 模型建立

2.1实验描述

本文以一复杂型材为例，型材截面尺寸如图1所示，该断面型材截面面积为390.4 mm²，最小壁厚为1.5 mm，最大壁厚为4 mm，各部分壁厚相差较大，且型材包含三个封闭内腔，模具要求在800 T挤压机上使用，挤压铝棒直径为120 mm，计算得到挤压比系数为29.0，模拟挤压速度为10 mm/s。

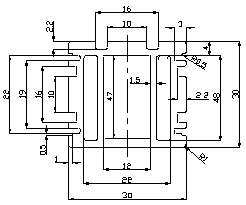
图1  复杂空心铝型材截面图

2.2几何模型和有限元模型的建立

2.2.1 几何模型

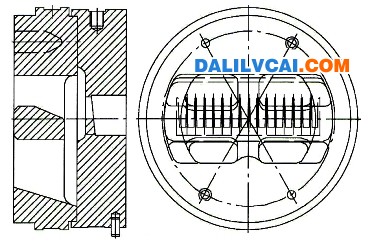
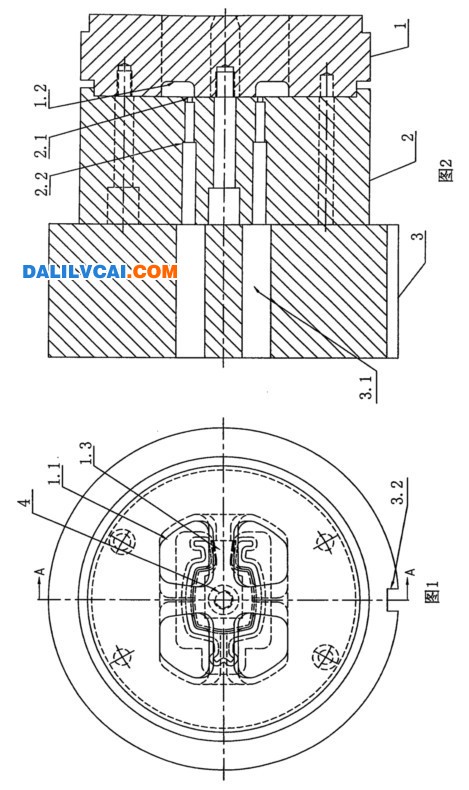
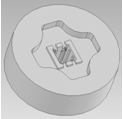
根据模具设计基本准则，该组合分流模具尺寸确定为：上模为Φ178×89 mm，下模为Φ178 mm×60 mm。由于型材截面的内腔被两条加强筋分为三个封闭的空心部分，该模具的设计一方面要满足型材两边离中心较远处边角的供料要求，另一方面又要保证有足够的材料流向加强筋的出口位置。图2为模具三维几何模型和实际加工出的模具，图3为工作带高度的设计方案。

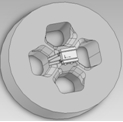
（a）复杂空心铝材挤压模具几何模型设计上、下模几何模型    

(a) Geometrical model of upper and lower die

（b）加工的上、下模

(b) manufactured upper and lower die

图2复杂空心铝材挤压模具上、下模模型

Figure 2 model of Upper die and lower die

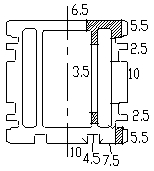
图3  复杂空心铝材挤压模具工作带高度分布

Figure 3 Land length distribution

2.2.2 有限元模型

挤压过程可分为初始、中间和末尾三个阶段，各阶段的金属流动状态是不同的，其中，开始挤压阶段和末尾挤压阶段为非稳态阶段，中间阶段挤出所需的型材产品，金属在模腔内为稳态流动状态，该阶段一般占用90%以上的挤压时间，也是生产出合格型材最重要的阶段，故本文忽略了前后两个非稳态阶段，只研究其中间阶段的金属流动情况，所以将分析模型中的毛坯设计成已经填充了模腔部分的挤出型材的形状^[2]。考虑到型材截面为对称结构，因此只取其1/2建立几何模型，然后，采用HyperMesh对三维几何模型划分有限元网格。

本文采用的铝合金材料AA6063的本构模型（modified Sellers-Tegart law）如下^[8]：

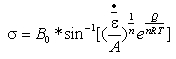                                                               (1)

式中：—流动应力；

—等效塑性应变速率；

R—气体常数，取R =8.314 J/(mol·K)；

T—温度；

B₀、A、Q和n分别是用来将流动应力适应于试验数据的参数，其中B₀25 MPa，A= 5.91×10⁹(1/s)，Q = 141550 (J/mol) 和n=5.385。

材料的弹性模量为3.681×10⁴MPa，密度为2.72ⅹ10³(kg/m³)，泊松比为0.333，热传导率为198 W/(m·K)，比热为900 J/(Kg·K)，坯料加热温度为750 K，模具和挤压筒预热温度为700 K。数值模拟的摩擦模型采用库仑模型，摩擦系数取0.4。

3 模拟结果与分析

由于稳态挤压阶段挤压速度恒定，各质点速度v_i与位移S_i成正比，即v_iS_i/t,t为挤压时间，所以金属速度场分布与位移场相同，图4为工作带出口位置和分流孔金属沿挤压方向（-z轴）的位移场分布图，由图可以看出，由于材料在分流孔内的分配很不均匀（右侧分流孔材料流动最快，中间分流孔最慢），导致出口截面的材料流动也很不均匀。

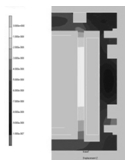
图4 复杂空心铝材工作带出口和分流孔的轴向位移分布

Figure 4 displacement distribution along the axis direction at bearing exit and pothole

产品断面上的各质点流出模孔工作带的速度均衡，这也是模具设计和维修遵循的基本原则。而挤压中常见的缺陷如波浪、扭拧、侧弯、面鼓或面凹等，都是由于模具设计没能满足金属挤出模孔速度均匀的要求。因此如何定量的评价流动速度的均匀程度，以及其对挤压过程能否获得合格产品的影响，对挤压模具的设计与使用有着重要的意义。本文提取型材出口处各质点的流速，进而求得模具出口处的标准速度场偏差——SDV值，并以此作为衡量金属流动是否均匀的判断依据，

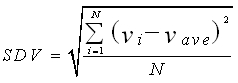                                                             (2)

式中：N—选取的节点数目；

v_i—出口截面上节点轴向流速；

v_ave—出口截面上所选节点平均轴向流速。

计算得到SDV的数值越小，说明材料的流动越均匀；SDV的数值越大，材料流动越不均匀。

将型材截面划分为32个区域，如图5(a)所示，并且取每个区域中心处节点的轴向位移代表该区域所有节点的平均轴向位移。图5(b)为选取节点的轴向流速，并以此作为各区域的平均轴向速度，整个截面的轴向平均速度v_ave为301 mm/s，而根据挤压比计算得到的理论挤出速度v为290 mm/s，二者仅相差3.8%，吻合非常好，进而计算得到轴向速度的SDV值为43.0，可以明显看出，截面出口的速度场分布很不均匀，其中平行于加强筋的边的中间位置速度最快，达到375 mm/s，加强筋的中间位置速度最慢，仅为219 mm/s。加强筋壁厚小，速度慢，可能会出现由于供料不足而导致挤出困难或尺寸偏小的缺陷。并且认为当型材材料出口速度波动在这一范围之内时，即SDV值小于某一特定值时，能保证模具成品不会出现由于设计环节造成的不合格产品。

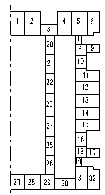
(a)             (b)

图5 复杂空心铝型材截面分区及其出口速度分布

Figure 5 Profile sectional subarea and velocity distribution at the exit

4  实验结果对比与分析

工作带出口流速的均匀程度对型材成型质量至关重要，流速越均匀，型材发生缺陷的可能性越小。根据该模具设计方案设计出的模具，经过试模获得料头如图6所示。与加强筋平行的两边挤出最快，两条加强筋挤出最慢，而且加强筋尺寸变薄，不能达到要求壁厚，对比有限元模拟分析结果可以看出，二者变形趋势非常吻合。

图6 试模后复杂铝型材料头

Figure 6 Profile remnant

结论

运用基于有限元法的模拟软件MSC.Marc对一复杂空心铝合金型材挤压过程进行数值模拟，在模拟过程中采用了一种既可以避免网格畸变和重划分，又能保证分析准确性的有限元模拟方法，研究了金属在模腔内的流动规律，利用出口质点轴向流速的SDV值定量的判定截面出口速度分布的均匀程度，揭示了金属的流动速度对产品形状及尺寸的影响，并将模拟仿真结果与试模结果进行比照分析，证明该方法可以成功地预测实际挤压过程中可能出现的潜在缺陷。
       
       （1）利用MSC.Marc对铝合金型材挤压过程进行数值模拟，并且提出了一种既可以避免网格畸变和重划分，又能保证分析准确性的有限元模拟方法，可以有效地模拟出挤压过程中材料的流动状态。

（2）利用出口质点流速的SDV值可以定量地判定截面出口速度分布的均匀程度，对照实际试模情况，认为当型材材料出口速度波动在这一个范围之内时，即SDV值小于某一特定值时，能保证生产出合格的型材。