1 前言
二辊可逆式热轧机因其结构简单，速度可调，正反向轧制，低速咬入、高速轧制，且容易实现机械化，劳动条件较好，便于采用大坯锭轧制，轧制规程调整灵便等优点被铝合金中厚板热轧制生产商广泛采用。在整个轧制过程中，确定轧制工艺参数，设计出合理的轧制规程是必不可少的环节，一般靠多次试轧或经验来确定相对合理的工艺参数。随着市场对产品质量要求的提高以及节能环保的要求，仅仅依靠传统的方法来确定轧制工艺参数显得不切实际。根据生产实际情况以及设备的能力确定合理的轧制工艺参数就必须建立轧制相关的数学模型，借助一些优化方法找出最优化的工艺参数，以此来确保产品质量，降低能耗，提高生产效率。
下面结合现场实际和操作经验，建立针对某厂可逆二辊轧机轧制数学模型，该数学模型包括轧制力模型、温降模型、辊缝模型、平直度模型、传动转矩和主电机功率模型、电机模型、前滑模型、轧制时间模型、电机发热模型、咬入条件等10个数学模型。
2 数学模型
2.1 轧制力模型
中厚板轧制过程中，每道次产生的宽展较小，近似于平面变形轧制，其宽展量可以忽略不计，因此轧制力计算可以采用Sims公式：
（1）
式中：
表示轧辊与板之间接触弧长；
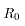表示变形区板的平均宽度，忽略宽展，
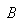为板料初轧宽度与终轧宽度和的平均值；
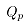为应力状态系数；
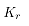为张力系数。
轧辊受到轧制力的作用而产生压扁，使得接触弧长增大，从而使得轧制力增加，其变化量一般在2%~3%左右，所以在计算轧制力时必须考虑轧辊压扁的影响。通常采用Hitchcock公式的简化形式：
（2，3）
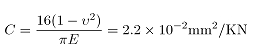（4）
式中：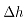
表示压下量；
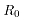表示轧辊初始半径；v表示轧件泊松比，为0.3；
表示轧辊弹性模量。
在计算轧辊压扁半径时，首先得知道轧制力大小，然而轧制力大小本身又与轧辊压扁半径有关，借助计算机编程，实现迭代算法，在一定精度下可以确定轧制力和轧辊压扁半径。具体算法如图1，图2为轧制3003铝合金板料时每道次轧辊压扁半径。
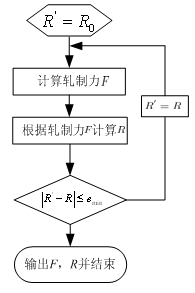
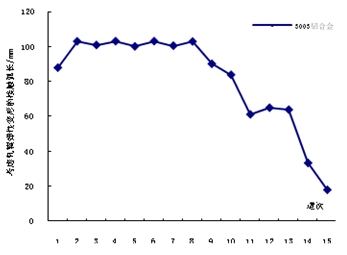
图1 考虑轧棍压扁半径的迭代算法 图2 3003铝合金与轧辊接触弧长
在有色金属加工行业中，对金属变形抗力模型的研究主要是通过实验室热模拟机测得实验数据，然后用数学回归的方法得出变形抗力模型。在实际生产中，许多未知因素干扰下，理论数据并不能直接用来指导生产，往往需要加上一些系数。通过现场测量，建立针对该厂轧制生产的铝合金变形抗力模型，并作为制定轧制规程的科学依据。变形抗力（）公式如下：
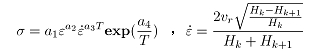（5，6）
式中：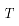
表示千分之一热力学温度；
表示工程应变，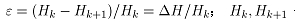
分别表示入口厚度和出口厚度；
表示轧辊转速；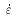
表示变形速度；
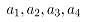都是待定系数。在反求变形抗力过程中往往要忽略一些将要的因素，比如轧辊的弹性压扁，有时要考虑最后几道次板料的加工硬化程度等等。
在实际计算轧制力过程中，通常用简化的Sims公式来计算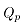
：
（7）
式中：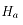
表示平均厚度，
。
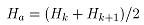铝板料未上卷时，可逆热轧中并没有张力，因此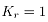
。张力计算公式如下：
（8）
式中：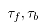
分别表示前后张力；
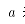表示平衡系数。当板料上卷后，发现后张力比前张力影响要大，
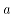的取值范围为
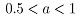，经过反复演算，认为在该轧制过程中取
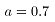较合适。
至此轧制力模型已完全建立，在实际生产中需要借助其它工具来完善，例如神经网络、专家系统和有限元模拟等。
2.2 温降模型
在铝合金热轧制过程中温度的预测一直以来都是个难题，影响温度的因素很多但问题主要集中在温度测量的准确度和难以确定的边界条件。铝合金热轧温度在600~550℃，终轧温度在280~320℃，不同牌号的铝合金轧制温度略有不同。与轧制薄带不同的是，中厚铝合金板轧件比较厚，轧件表层和中心温度较大，但是其从头到尾的温度梯度不是很显。
通常坯料出炉到终轧，温度的变化是由坯料辐射散热、与空气对流散热、与乳化液对流散热、与轧辊接触换热、与辊道接触换热以及轧件变形生热。在实际生产过程中，坯料与空气对流散热可以看作辐射散热，一般情况下相当于辐射散热的10%，故在建立模型时仅在辐射散模型中添加系数修正。另外，考虑到轧辊与坯料接触面积小、时间短，其散热量可以忽略不计。
辐射散热公式是根据波尔兹曼方程：
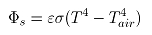（9）
其中：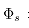
表示热流密度，
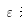表示铝合金板的灰度，
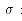表示斯特潘－波尔兹曼常数（也叫作辐射系数），T为物体热力学温度，
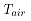为空气热力学温度（下文中温度若不特殊说明皆为气力学温度）。联立热平衡方程：
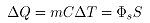（10）
其中：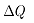
为辐射热量变化值；m为质量；
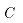为比热容；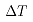
为温降；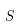
为坯料的表面积。考虑到侧面积很小，计算面积时忽略侧面积，只计算上下表面。另外考虑温度随时间变化，因此积分后可得出辐射温降方程：
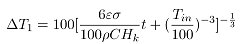（11）
其中：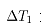
为因辐射引起的温降；
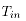表示坯料入口温度；
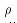表示铝合金的密度；
表示轧件厚度；ｔ表示辐射时间。根据生产实际总结的经验，铝合金热轧时辐射系数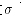
可取0.2。由于实际试验过程中第13道次单边上卷，第14、15道次双边上卷，辐射系数将发生变化。为表达这一变化用
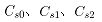分别表示无上卷系数、单边上卷系数、双边上卷系数。公式（11）中的
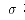将变为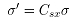
，
取0，1，2。根据长期实践积累，无上卷、单边上卷、双边上卷系数分别为1、0.75、0.5。
浮化液对流散热可以近似看作低压喷水冷却，对流换热可由牛顿对流换热公式：
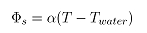（12）
将公式（12）代入公式（10）中便可得出浮化液对流散热模型：
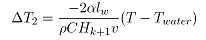（13）
式中：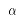
为对流系数，取
，
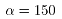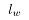为浮化液作用长度，测得
；
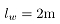为铝合金密度；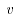
表示轧件出口速度，一般要考虑前滑值，则
，
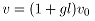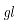为前滑值，
为轧辊线速度。
接触换热是指轧件与设备接触而传递热量引起温降。以轧件为研究对象，考虑到轧件与导辊接触时间短、温差较小等因素，略去轧辊与导辊之间的接触换热。轧辊在乳化液的冷却作用下，温度较低，轧件与轧辊之间的接触换热较明显。处理现场测得的数据，回归出接触换热公式：
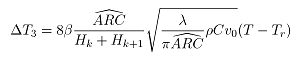（14）
其中：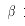
为轧件与轧辊热传导率系数，取
；
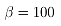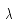为接触热传导系数；
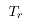为轧辊的温度。
轧制过程中坯料发生塑性变形过程中，轧辊传递机械能使轧件发生变形，同时会伴有金属加工硬化，而且在随后的再结晶过程中，加工硬化组织中积累的机械能会以热能的形式释放出来，使轧件温度升高。由此造成的温升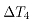
:
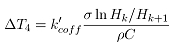(15)
其中：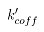
为功转化为热的有效系数，需要根据现场实际选取。
至此铝合热轧温降模型全部建立，综合以上公式（11）、（13）、（14）、（15）可得出每道次铝板出口温度：
（16）
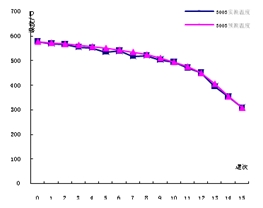
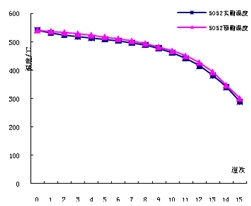
图3 3003系铝合金实测与预测温度 图4 5052系铝合金实测与预测温度
2.3 辊缝模型
在板带轧制中最重要的指标是良好的板型，获得良好板型就必须建立合适的辊缝模型。通常，先进的轧机配备有AGC系统、弯辊装置以及自学习系统，有时还要考虑轧机的弹跳。在实际的生产中，控制板材的凸度和板型是通过控制轧辊的凸度来实现的，针对该厂二辊可逆热轧机没有AGC、弯辊装置、上辊为凹辊、下辊为平辊等特点，建立简单而又实用的辊缝形状方程。可以用下面的方程表示：
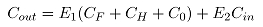（17）
其中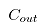
表示出口凸度，
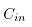表示入口凸度，
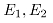表示影响因子，
表示轧制力引起两辊的凸度，
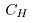表示两轧辊热凸度，
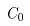表示上辊凹陷值。
2.4 平直度模型
在实际轧制生产中用板坯的平直度来描述其板形，即板材是否产生波浪、翘曲、侧弯等。根据长期经验总结，热轧过程中轧制力过大往往容易产生边浪，过小容易产生中浪。图5表示平直度与轧制力之间的关系。
保持板形良好的条件为：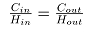
，但在实际生产中，由于现场复杂，很难保证每个道次都满足以上条件，因此板料或多或少会有一定的不平整，通常将相对误差
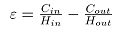控制在很小的范围内（
）。
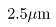2.5 传动转矩及主电机的功率模型
两辊可逆热轧机轧制过程中，主电机输出的扭矩用于克服以下4个方面的阻力矩：铝材轧制力矩（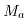
）、轧机空转力矩（
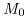）、传动过程中损失的力矩（
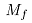）、轧机减速或加速运行时克服惯性力矩（
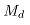），用公式表示为：
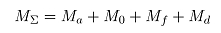（18）
空转力矩通常是根据空载工况下的电流确定，经现场测试，可取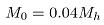
，其中
为轧机电机的额定力矩。传动过程中损失的力矩可以用以下公式计算：
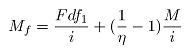（19）
其中：ｄ为轧辊辊颈直径；ｉ为传动比，取11.5；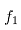
为轴承的摩擦系数，查手册为0.004，Ｍ为轧制力矩；
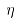为传动装置的效率，取0.95。
在轧制过程中前几道次坯料很短，整个过程都处于变速阶段，克服惯性矩需要的力矩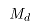
计算公式如下：
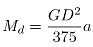（20）
其中：Ｇ表示轧辊重量；Ｄ表示轧辊的有效直径；ａ表示加速度，实测得咬入阶段的加速为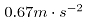
，甩出阶段加速度为
。
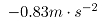确定轧制力矩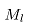
通常采用的方法有按金属在轧辊上的轧制力作用来计算轧制力矩，或者计算轧辊上的切向摩擦力来计算轧制力矩，也可按积累的实际能耗数据来估算。在本次试验中采用第二种方法，即：
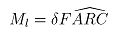（21）
其中：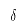
为力臂系数，对热轧制工艺通常取0.42~0.5。
尽管试验中采取用电机发热来校核设备是否过载，但依然要对力矩是否超过额定力矩进行校核，就需要计算等效力矩（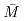
）：
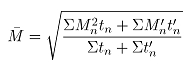（22）
其中：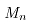
为道次轧制时的力矩；
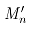为每道次后空载力矩；
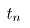为轧制时间；
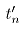为空载时间。
电动机升温的条件是：等效力矩大于等于额定力矩，即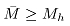
，电动机过载的条件是：轧制阶段的最大力矩大于等于电机的安全力矩，即
，其中ｋ取2.0~2.5。
电机功率模型采用以下公式计算：
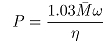（23）
其中：Ｐ为电机功率；ｗ为电机转速；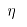
为电机到轧机的传动效率，取0.96。
2.6 电机模型
电机输出转矩，但转矩必须满足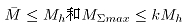
，为此根据直流电机功率计算公式：
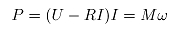（24）
其中：Ｕ为电机电压；Ｒ为电机内阻；Ｉ为电机电枢电流；Ｔ为电机扭矩；ｗ为电机转速。
由图6可知，当电机速度在基速以上时，电机恒功率运行，此时电机电流随转速的增加而增加，电机提供的扭矩可以根据额定功率与转速求出；当电机在基速以下工作时，电机输出的转矩非常大，但要满足上文中提到的条件。电机在恒功率模式下运行时，满足以下公式：
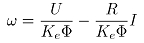（25）
其中：
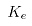与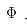
只跟电机的内部构造有关，可从电机相关手册上获得。
2.7 前滑模型
在铝合金热轧过程中，常出现出口速度大于轧辊线速度的情况，特别在上卷过程中更明显，实际轧制过程中，前滑值一般在2%~10%。影响前滑的因素主要有轧辊直径、摩擦系数、轧件厚度、前张力和加工率。根据Sims公式可以推导出前滑公式：
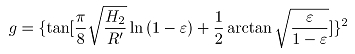（26）
其中：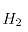
为轧件出口厚度；
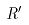为轧辊压扁半径；
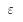为加工率。
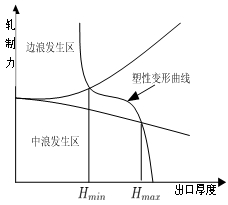
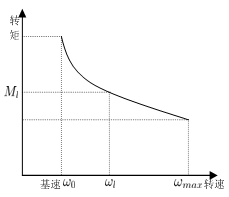
图5 平直度与轧制力之间的关系 图6 电机转矩与转速关系
2.8 轧制时间模型
校核电机发热、计算热辐射时，时间是非常重要的参数，同时轧制时间的长短也是衡量轧制规程是否合理的一个方面。时间模型可分为咬入阶段、咬入加速阶段、稳定轧制阶段、甩尾减速阶段和甩出后阶段。实际生产过程中，咬入阶段和甩出后阶段时间很短，约2~5秒，在计算中可将其忽略，轧制时间如图7所示。其中，
为咬入前阶段，
为咬入加速阶段，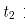
为稳定轧制阶段，
为甩尾减速阶段，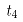
为甩出后阶段，
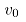为咬入速度，
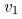为甩尾速度，
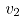为稳定轧制速度，
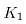为加速阶段的加速度，厂商提供的是
，
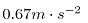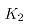为减速阶段的加速度，厂商提供的是
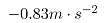，单道次轧制总时间ｔ为：
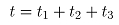。每个阶段的轧制时间计算公式如下：
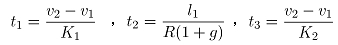（27，28，29）
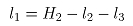（30）
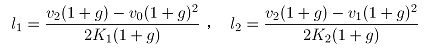（31，32）
其中：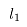
表示咬入加速阶段的坯料长度，
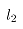表示甩尾阶段的坯料长度，
表示出口厚度，ｇ为前滑值。
2.9 电机发热校核模型
为发挥电机的潜能，人为地让电机在极限工况下工作，所以电机是否过载是本试验中始终关注的内容。目前在国内校核电机主要比较实际功率与额定功率，若实际功率高于额定功率则认为电机过载。但在实际计算过程中，实际功率往往不容易计算，本文借鉴国外学者校核电机过载的方法，提出采用电机发热量来校核电机是否过载，这样可有效地发挥电机潜能。
电机自身可容纳的最大热量为临界值，其计算公式为：
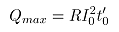（33）
其中Ｒ为电机内阻，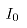
为电机可承受的最大电流，
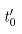为时间常数，直流电机一般取300~600秒。
实际轧制过程中电机的发热量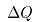
为：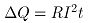
很显然电机不过载的条件为：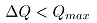
实际轧制过程中也包含电机散热，考虑到极限情况，忽略轧制时的散热，只考虑在间歇时间的散热
：
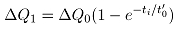（34）
其中：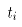
为上一道次与下一道次之间的间歇时间。
2.10 咬入条件模型
整个轧制过程能否进行首先要满足咬入条件，因此必须建立咬入条件来作为约束轧制规程的制定。轧辊与坯料之间的摩擦力是咬入的动力最重要的关系，其关系如图8所示。只要咬入角α小于摩擦角β的时候才能咬入，也即满足：
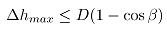
其中：D为轧辊直径，
为绝对压下量，由预定工艺确定。
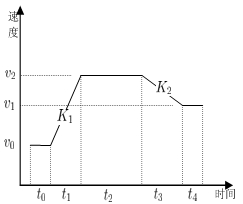
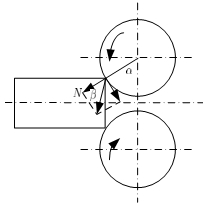
图7 轧制时间示意图 图8 咬入角与摩擦角的关系
3 实验分析
采用计算机编程实现上述建立的数学模型，并进行优化，最终制定出最优的轧制规程。通过在现场试轧制，验证了优化后的规程。该优化规程在保证板形良好的情况下，同时能实现减少轧制道次，节省时间，减少功耗。表1是针对3003铝合金原先规程与优化后规程的对比。
表1 3003铝合金轧制工艺对比
|
总道次 |
最大压下量 |
最小压下量 |
耗时 |
能耗 |
|
|
原先规程 |
15 |
30mm |
7.2mm |
609.9s |
52.75Kwh |
|
优化后规程 |
13 |
30mm |
0.8mm |
422.3s |
41.1Kwh |
通过对比可发现，在其它工艺条件相同的情况下轧制同样的坯料，优化后的轧制规程可明显地降低能耗，约22.1%，节省时间约187.6秒。
4 结论
针对某铝合金中厚板生产厂商可逆二辊轧机，通过现场测量铝合金热轧相关工艺参数，通过反求并用数学回归方法建立符合实际轧制过程的数学模型。建立的数学模型和实际测量数据能很好地吻合，在此基础上提出一种确定轧制规程的方法。该方法提出用电机发热量来判断电机是否过载，在实际应用中，用该方法计算出的轧制规程能很好地保证铝合金产品板型，最大限度地挖掘轧机潜能，提高生产效率。
（1）针对具体的轧制生产线建立合适的数学模型是优化其规程的前提条件。在建模中要充分利用各种数学工具和先进的测试手段，才能更加准确地建立数学模型，为优化提供条件。
（2）提出用电机发热校核电机是否过载，能有效地发挥电机的潜能，提高能源利用率。
