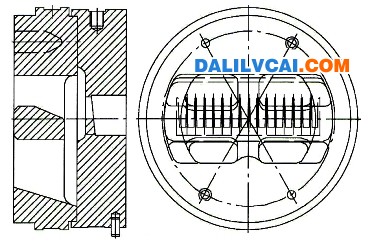
导流模又称前室模,是生产薄壁复杂实心型材常用的挤压模具。采用导流模具生产型材时,坯料首先通过导流孔预成形,获得与型材相似的几何形状,然后再进行二次变形,挤压出各种断面形状的型材。导流孔不仅增大了坯料与型材的几何相似性,有效地控制了金属流动,减少了产品的扭拧和弯曲变形,而且改善了模具的受力条件,提高了模具寿命,所以其设计是否合理是导流模具设计的关键。传统模具设计主要依赖设计者的经验,经过反复试模修模,最后生产出合格零件,既费时又费力。利用数值仿真的方法不仅周期短、成本低,而且可以获得材料的应力、应变、温度、速度等现场难以测量的场量,对于掌握挤压过程中材料在模具中的流动规律进而提高型材质量非常重要。为此,国内外许多学者采用数值模拟的方法对挤压成形过程进行了大量的研究,并取得了较大的进展。
目前关于挤压过程的数值模拟研究大多采用拉格朗日法和欧拉法。采用拉格朗日法分析大变形的挤压问题时,单元容易产生畸变,需要频繁的网格重划,导致体积损失过大,严重影响了计算精度;而采用欧拉法模拟时,需要利用复杂的数学映射来描述自由表面的运动状况并且对材料所有可能流过的区域划分网格,占用大量计算机内存,特别是分析薄壁、空心、复杂断面型材时计算时间令人难以接受。ALE(Arbitrary Lagrangian Eulerian, ALE) 算法吸收了拉格朗日和欧拉算法的优点,通过引入一个独立于物质构型和空间构型的参考构型,使得计算网格能够任意移动,从而避免了单元畸变以及自由界面追踪所带来的困难。本文采用基于ALE算法的商业化软件HyperXtrude对一异形铝型材的挤压过程进行数值模拟,以导流孔形状为影响因素,采用Box-Behnken设计确定试验方案建立分析模型,利用最小二乘法对模拟结果进行拟合,得到型材截面速度均方差的响应曲面公式,并以此为优化目标采用粒子群算法对导流孔形状进行优化。
导流模又称前室模,是生产薄壁复杂实心型材常用的挤压模具。采用导流模具生产型材时,坯料首先通过导流孔预成形,获得与型材相似的几何形状,然后再进行二次变形,挤压出各种断面形状的型材。导流孔不仅增大了坯料与型材的几何相似性,有效地控制了金属流动,减少了产品的扭拧和弯曲变形,而且改善了模具的受力条件,提高了模具寿命,所以其设计是否合理是导流模具设计的关键。传统模具设计主要依赖设计者的经验,经过反复试模修模,最后生产出合格零件,既费时又费力。利用数值仿真的方法不仅周期短、成本低,而且可以获得材料的应力、应变、温度、速度等现场难以测量的场量,对于掌握挤压过程中材料在模具中的流动规律进而提高型材质量非常重要。为此,国内外许多学者采用数值模拟的方法对挤压成形过程进行了大量的研究,并取得了较大的进展。
目前关于挤压过程的数值模拟研究大多采用拉格朗日法和欧拉法。采用拉格朗日法分析大变形的挤压问题时,单元容易产生畸变,需要频繁的网格重划,导致体积损失过大,严重影响了计算精度;而采用欧拉法模拟时,需要利用复杂的数学映射来描述自由表面的运动状况并且对材料所有可能流过的区域划分网格,占用大量计算机内存,特别是分析薄壁、空心、复杂断面型材时计算时间令人难以接受。ALE(Arbitrary Lagrangian Eulerian, ALE) 算法吸收了拉格朗日和欧拉算法的优点,通过引入一个独立于物质构型和空间构型的参考构型,使得计算网格能够任意移动,从而避免了单元畸变以及自由界面追踪所带来的困难。本文采用基于ALE算法的商业化软件HyperXtrude对一异形铝型材的挤压过程进行数值模拟,以导流孔形状为影响因素,采用Box-Behnken设计确定试验方案建立分析模型,利用最小二乘法对模拟结果进行拟合,得到型材截面速度均方差的响应曲面公式,并以此为优化目标采用粒子群算法对导流孔形状进行优化。
2 优化模型的相关理论
2.1 ALE算法基本理论
ALE算法以物质运动的ALE模型为理论基础,不同于拉格朗日或欧拉描述模型,ALE模型另外引进了一个独立于物质构型(ΩX)和空间构型(Ωx)的参考构型(Ωξ)。计算网格的划分是在参考构型中进行的,独立于物体和空间运动的,可以根据需要自由选择。根据任意单元体中的质量、动量和能量守恒定律,获得参考坐标系下的控制方程:
质量守恒方程:
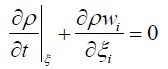
动量守恒方程:
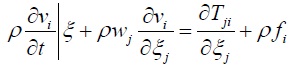
能量守恒方程:
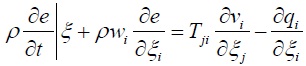
式中ρ为材料的密度,wi、wj为物质点在ξ空间中的位置矢量对时间的导数,vi为物质点在空间中的速度矢量,Tji为定义在参考构型下的第一类皮奥拉-克希荷夫应力张量,fi为作用于物体中单位质量的体力,e为物体单位质量中的内能。
在采用ALE算法求解具体问题时,需要引入正确的材料本构关系并对模型施加适当的边界条件,然后对整个控制方程进行求解。
2.2 响应曲面模型和Box-Behnken试验设计
响应曲面法(response surface methodology, RSM),也称回归设计,是采用多元二次回归方程来拟合因素和响应值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变量问题的一种统计方法。RSM法与其他数据统计方法相比,不仅考虑了自变量之间的交互作用,提高了拟合精度,而且还可以运用图形技术将二者之间的函数关系显示出来,使结果更加直观。本文选择二阶响应曲面方程,其模型可表示为:
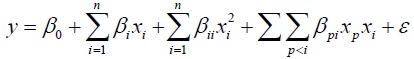
式中,xi为设计变量,ε为残余误差,βo、βi、βii、βpi均为待定系数。
Box-Behnken试验设计是一种基于三水平的二阶试验设计方法,可以评价指标和因素之间的非线性关系,是RSM常用的试验设计方法之一。Box-Behnken设计的每个因素只需要三个水平,与其他方法(如星点设计法)相比所需的试验次数较少,效率更高,且所有的影响因素不会同时处于高水平,所有的试验点都落在安全区域内,因此本文选取Box-Behnken试验设计方法对导流孔的形状进行优化设计。
2.3 PSO算法基本原理
粒子群优化算法(particle swarm optimization, PSO)是Kennedy和Eberhart于1995年提出的一种以鸟类觅食行为为基础的全局优化算法,因其原理简单,算法实现容易,运行速度快,已被广泛应用于机械、化工、生物医学等领域。该算法模仿鸟类的群体觅食过程,将待优化问题的解看作为搜索空间中的一个粒子(鸟),解的优劣程度由适应函数决定。各粒子通过不断追踪自身所经过的最佳位置和整个种群所经过的最佳位置这两个极值来更新自己的速度和位置,最终到达全局最优解所在的位置。
3 模拟试验方案的确定
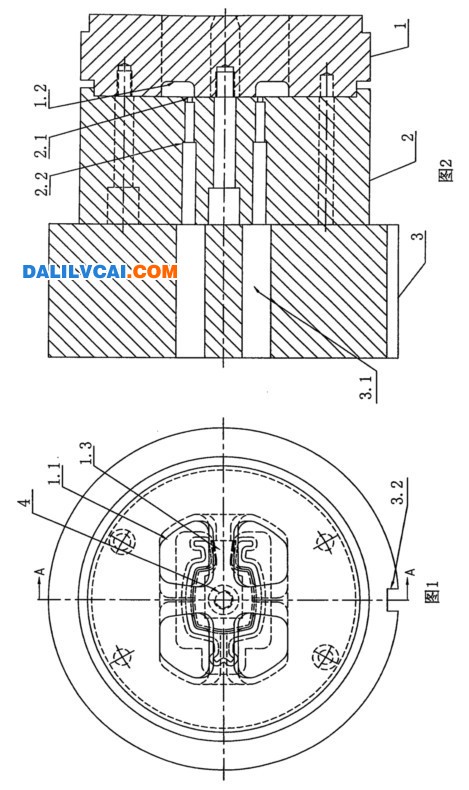
为了获得最优的导流孔形状,进而更好地控制材料在模具中的流动,提高型材质量,在保持其他工艺参数不变的情况下,选取导流孔不同部位的宽度作为优化变量,如图1所示,并结合实际情况确定各个变量的范围如表1所示。以模具出口型材截面上的金属流速均方差(SDV)为优化目标,建立优化模型如下:
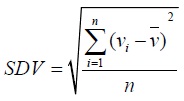
式中,n为所考虑截面内的节点个数;vi为出口截面上第i个节点的流速;v为出口截面上所有节点的平均流速。
表1 设计变量及其取值范围
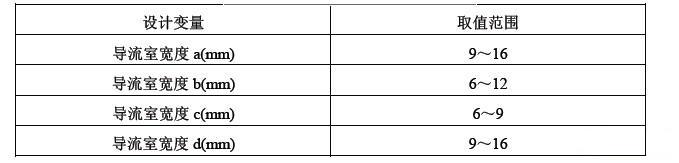
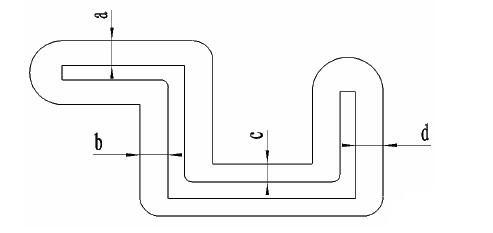
图1 设计变量的位置
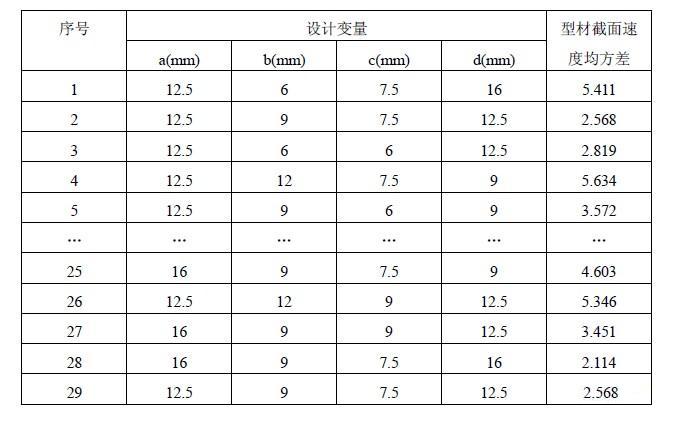
选取6063铝合金作为模拟材料,挤压筒预热温度为450℃,坯料加热温度为480℃,挤压比为31.2,模具与坯料间的对流换热系数为3000 W/m2·℃,挤压速度为2mm/s,模具工作带处设为库仑摩擦,摩擦系数为0.3,其他部位设置为粘性摩擦。将材料流经区域分为棒料、导流孔、工作带和型材四个部分进行网格划分,并建立分析模型如图2所示,其中工作带和型材部分采用三棱柱网格,导流孔和棒料部分采用四面体网格。将上述4个设计变量在各自范围内取3个水平,采用Box-Behnken设计确定试验方案,对所设计29组试验方案进行数值模拟,并计算出相应的型材出口流速均方差,如表2所示(由于数据较多,在此只列出部分结果)。

图2 分析模型
表2 Box-Behnken试验设计表及计算结果
4 响应曲面的建立和粒子群算法寻优
根据表2中的数据,利用最小二乘法拟合响应曲面,得到型材出口速度均方差与导流孔形状的响应面函数如下:
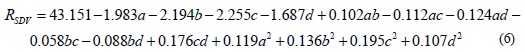
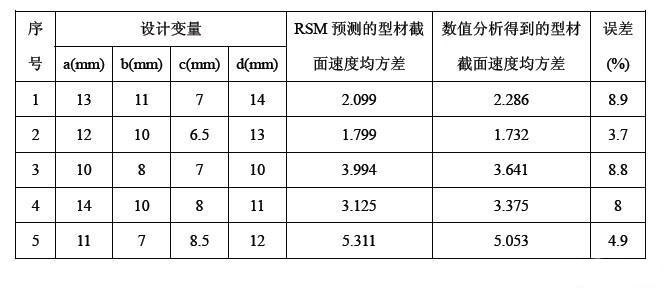
表3为本文模型的方差分析结果,模型较小的P值表明回归模型对响应值的影响极为显著;相关系数R-Squared为0.9864,表明模型拟合程度良好,误差较小,可以用来拟合实验结果。为了进一步验证RSM预测结果与数值分析结果是否一致,本文另外设计五组试验进行数值模拟,并与RSM预测结果进行比较,如表4所示,预测值与模拟结果之间的误差均小于10%,说明RSM的预测结果比较准确,与实际情况比较吻合。
表3 二阶模型的方差分析
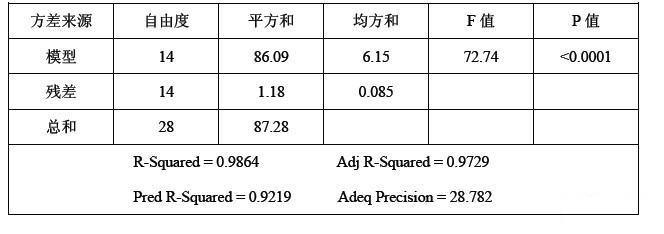
表4 RSM预测结果与数值分析结果的比较
为了获得最佳的导流孔形状参数,结合粒子群优化算法对上述响应面模型寻优,设置初始种群数目为40,惯性权重取0.8,学习因子取1.45,最大迭代次数为200。进化迭代次数与适应度值之间的关系如图3所示,迭代20次左右,粒子达到最佳位置,得到最优导流孔形状参数为a=15.58;b=8.45;c=6;d=15.47,此时RSM预测的型材截面速度均方差为0.35。
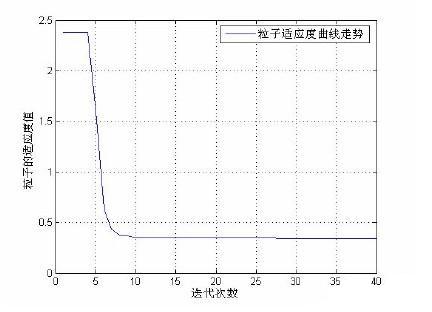
图3 粒子群优化算法进化代数与适应度值关系
5 优化结果与讨论
为了验证优化结果的正确性,根据优化后的模具结构参数建模并进行数值模拟,得到的模具出口型材截面速度均方差为0.38,与RSM所预测的结果0.35几乎一致。模具优化后型材截面速度分布与初始设计方案对比如图4所示,可以看出初始设计方案中型材挤出模具后产生了较大的变形,尤其在几个角上变形尤为明显,而优化后型材变形明显减小。在整体速度分布对比上,优化后模具出口处型材截面最大速度与最小速度之差仅为1.5mm/s,而初始计方案中的最大速度与最小速度差值达到20mm/s,速度均方差为5.4。在挤压力方面,优化后导流孔对材料的分配更加合理,更有利于控制材料流动,因此成形所需的挤压力(5710kN)较初始方案(5980kN)降低了5%。图5为优化后型材截面的温度分布图,可以看出整个型材截面上温度分布比较均匀,最高温度与最低温度的差值仅为10℃,完全符合实际生产的要求,也为获得高质量型材提供了保证。综上所述,采用数值模拟结合响应曲面法和粒子群算法对导流孔形状进行优化是可行的,模具优化后不仅改善了金属流动情况,减小了型材的变形,提高了型材质量,而且还降低了挤压力,减少了能耗,从而为企业的实际生产过程提供了技术支撑。
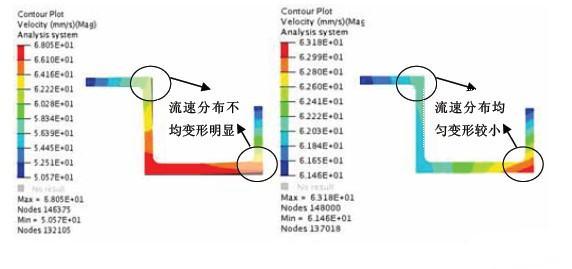
图4 初始方案与优化方案的速度对比图
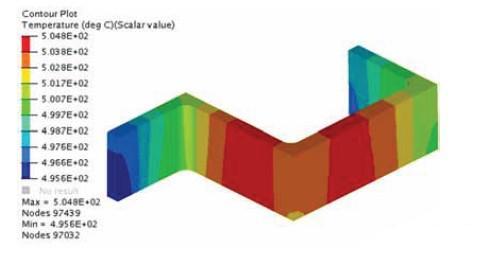
图5 模具出口处铝型材的温度分布图
6 结论
(1) 采用基于ALE算法的HyperXtrude软件对一异形铝型材挤压过程进行了数值分析,得到了型材的速度、温度分布和变形情况,分析了金属在挤压过程中的流动规律。
(2) 以导流孔形状为影响因素,以模具出口型材截面的速度均方差为优化目标,采用Box-Behnken设计确定试验方案,结合曲面响应法和粒子群算法对铝型材导流孔形状进行了优化。
(3) 与初始模具设计方案相比,模具优化后挤出的型材速度分布更加均匀,变形明显减小,模具出口型材截面的速度均方差为0.38,仅为初始设计方案的7%,大大提高了铝型材的质量。